목차
1. ROC curve, AUC
2. titanic 실습(sklearn 코드)
지난 시간에 분류문제의 성능평가 지표인 Accuarcy, Recall, Precision, F1 score에 대해서 알아보았다. 오늘은 ROC curve에 대해서 알아보겠다. (참고 : 분류문제 성능평가 지표: Accuracy, Recall, Precision, F1 score (+titanic 실습))
1. ROC curve, AUC
ROC(Receiver Operating Characteristics) curve란, 종속변수값을 무엇으로 예측할 것인지의 기준이 되는 확률(threshold probability) 값에 따른 TPR과 FPR값들의 집합을 의미한다. 그리고 AUC(Area Under the Curve)는 ROC curve 아래의 면적을 의미하며, 모델의 성능을 나타냅니다. ROC, AUC는 모델 성능을 비교할 때, threshold를 바꿔도 전반적인 성능이 좋고 나쁘고를 비교하고 싶을 때 사용한다.(threshold에 대한 설명은 아래 나옵니다.)
여기서 TPR은 True Positive Rate의 약자로, recall에서의 sensitivity를 뜻한다. 즉, 실제 positive 관측치 중에서 positive로 정확히 예측된 관측치의 비중을 나타낸다.
FPR은 False Positive Rate의 약자로, 실제 negative 관측치 중에서 positive로 잘못 예측된 관측치의 비중을 나타낸다.
식으로만 보면 직관적으로 이해가 잘 안되서 그림을 그려봤다. 아래 그림을 참고하면 이해가 직관적으로 될 것이다.

만약 여기서 TPR도 1이고, FPR도 1이면 어떻게 될까? 모든 positive 데이터에 대해서는 정확하게 예측했지만, 모든 negative 데이터에 대해서는 positive 데이터로 오답을 예측한 결과가 된다. 그럼 가장 좋은 지표는 무엇일까? TPR이 1이고, FPR은 0일 때 모든 데이터가 100% 정확하게 분류됐다는 뜻이다. 로지스틱 회귀모형으로 예로 들면, 아래 그래프와 같은 상황이 된다. 주황색 점선은 threshold를 의미하는데, 이게 0인 지점에서는 y(빨간색, 검정색 X point)가 0보다 작은 수는 negative로 예측하고, 0보다 큰 수는 positive로 예측한다. 그럼 threshold를 0.5로 설정하면 어떻게 될까?

이러한 데이터의 경우엔 threshold를 0.5로 설정하면, 아래 그래프와 같이 모든 데이터가 100% 정확하게 분류가 된다.(주황색 점선 아래로는 negative, 위로는 positive로 예측하기 때문에) 이 케이스는 threshold를 0.2~0.8로 설정했을 때(더 보기 참고), TPR이 1이고, FPR이 0이 되는 것이다.



이 분류 성능을 나타내는 지표가 바로 ROC curve이다. TPR을 y축으로, FPR을 x축으로 해서 그래프로 나타낼 수 있다. threshold가 0일때, 0.1일 때, 0.2일 때,..., 1일 때의 경우를 모두 아래 그래프에 점을 찍어서 연결시키면 ROC curve가 된다. 이 그래프에서 AUC 영역이 1이 됐을 때, 즉 정사각형이 됐을 때가 가장 좋은 성능이 나타나는 케이스다. 우리가 위 그래프에서 봤던 것처럼 threshold을 일정 범위로 설정했을 때, 100% 데이터가 분리되는 경우에만 AUC의 넓이가 1이 된다. 만약 (-0.5,0) 벡터에 있던 negative 데이터 하나가 (0.5,0) 벡터로 옮겨지고, (0.5,1) 벡터에 있던 positive 데이터 하나가 (-0.5,1) 벡터로 옮겨진다면, 아래 그래프와 비슷하게 curve형태가 나오는 그래프가 된다.(물론 데이터 양이 훨씬 많아야 곡선 모양이 된다.)

ROC curve, AUC 성능 지표를 쓰는 목적은 크게 2가지이다.
1. 이진 분류 모델끼리 전반적인 성능 비교
2. optimal threshold을 찾고 싶을 때(즉, postive와 negative를 가장 잘 분류하는 확률 기준을 찾고 싶을 때)
2. titanic 실습(sklearn 코드)
저번 시간에 진행했던 titanic 실습에 이어서 ROC curve, AUC도 만들어보겠다. (아래 포스트 참고)
분류문제 성능평가 지표: Accuracy, Recall, Precision, F1 score (+titanic 실습)
목차: 1. 분류문제 성능평가 지표 1-1. Confusion matrix 1-2. Accuracy(정확도) 1-3. Recall(재현율) 1-4. Precision(정밀도) 1-5. F1 score 2. 데이터 불균형 문제 2-1. Over sampling 2-2. Under sampling 3. 케글 titanic 실습 분류
coduking.tistory.com
저번에 데이터 전처리까지 모두 끝낸 후, train_test_split()함수를 통해서 학습, 평가 데이터를 분리시켰다. 분리시킨 데이터 중에 독립변수를 min-max정규화를 시켰고, 로지스틱 회귀 모형을 lr이라는 변수이름으로 할당해 주어 학습시켜서 성능평가하는 단계까지 진행했다.
y_prob = lr.predict_proba(X_val_minmax)
# ex
# array([[0.87247488, 0.12752512],
# [0.87247488, 0.12752512],
# [0.59794491, 0.40205509],
# [0.48097866, 0.51902134],
# [0.87247488, 0.12752512],
# [0.48097866, 0.51902134]])
predict_proba 함수를 사용하면, 각 클래스의 확률을 예측할 수 있다. 확률 예측이기 때문에 분류문제에서만 사용할 수 있다. 값은 0~1 사이의 값이 나온다. 위 코드는 minmax정규화를 시킨 검증용 feature들이 1~0 사이에 어떤 확률을 가지는지를(위 로지스틱 모델 예시 그래프에서 X point를 생각해 보자) 예측해 주는 코드이다. y_prob에는 y가 1일 확률과 0일 확률을 각각 나타내는 값이 담긴 2차원 배열 형태가 저장된다.
from sklearn.metrics import roc_curve
# roc curve for models
fpr1, tpr1, thresh1 = roc_curve(y_val, y_prob[:,1], pos_label=1)
sklearn의 metrics 클래스에서 roc_curve 함수를 통해서 반환된 FPR, TPR, threshold를 각각 변수에 할당해준다. 이때, roc_curve()함수 안에 들어가는 파라미터의 순서는 다음과 같다.
sklearn.metrics.roc_curve(y_true, y_score, *, pos_label=None, sample_weight=None, drop_intermediate=True)[source]- y_true: 실제 클래스 값 array(array shape = [데이터 건수])
- y_score: predice_proba()의 반환 값 array에서 Positive 칼럼의 예측 확률이 보통 사용 됨.
- pos_label: positive label을 어떤 값으로 설정할 것인지.
참고로, y_score에 y_prob[:,1]를 썼다는 건 독립변수가 1인 값, 즉 positive 관측치를 기준으로 보겠다는 뜻이다. 이제 ROC curve를 그려보겠다.
import matplotlib.pyplot as plt
plt.style.use('seaborn')
# plot roc curves
plt.plot(fpr1, tpr1,color='orange', label='Logistic Regression')
# title
plt.title('ROC curve')
# x label
plt.xlabel('False Positive Rate')
# y label
plt.ylabel('True Positive rate')
plt.legend(loc='best')
plt.savefig('ROC',dpi=300)
plt.show()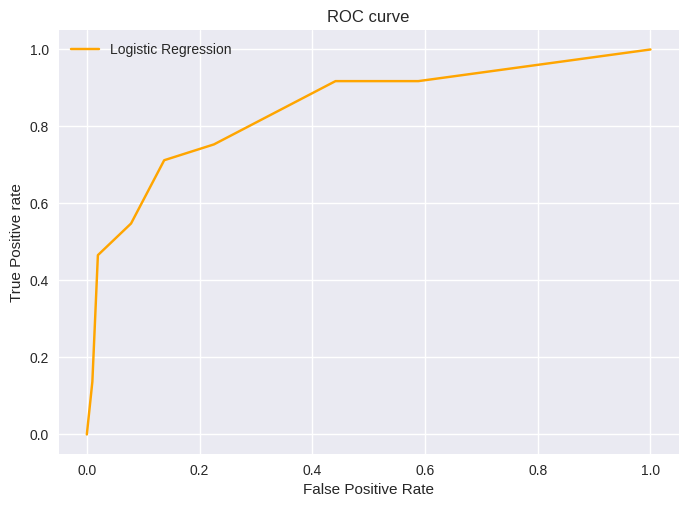
이렇게 ROC curve를 그래프로 확인할 수 있는 실습까지 진행해 보았다. 마지막으로 AUC이 넓이를 구할 때는 아래 코드를 구할 수 있다. 1에 가까울수록 성능이 좋다는 뜻이다.
from sklearn.metrics import roc_auc_score
# auc scores
auc_score1 = roc_auc_score(y_val, y_prob[:,1])
print(auc_score1)
'통계, AI' 카테고리의 다른 글
| Perceptron, Multi-Layer Perceptron, Activation function 정리 (0) | 2023.07.07 |
|---|---|
| Output function, Loss function(feat. 소프트맥스, 크로스 엔트로피) (0) | 2023.07.05 |
| 분류문제 성능평가 지표: Accuracy, Recall, Precision, F1 score (+titanic 실습) (1) | 2023.06.10 |
| [로지스틱 회귀] Solver 종류와 장단점 (2) | 2023.06.07 |
| 원-핫 인코딩: pd.get_dummies() vs OneHotEncoder() (2) | 2023.06.06 |



댓글