목차:
1. 분류문제 성능평가 지표
1-1. Confusion matrix
1-2. Accuracy(정확도)
1-3. Recall(재현율)
1-4. Precision(정밀도)
1-5. F1 score
2. 데이터 불균형 문제
2-1. Over sampling
2-2. Under sampling
3. 케글 titanic 실습
분류문제의 성능평가 지표에는 Accuracy, recall, precision, F1 등이 있다. 이는 모델 평가단계에서 사용하는 성능평가 지표이다. 이번시간에는 가장 대표적인 평가지표인 4가지에 대해서 먼저 알아보겠다.
위에서 언급한 4개의 분류문제 성능평가지표는 계산을 위해서 confusion matrix를 사용해야 한다. 이는 종속변수의 실제값과 모형을 통해서 예측이 된 종속변수 값에 따른 관측치들의 분포를 나타내는 matrix이다.

1-1. Confusion matrix
Confusion matrix는 아래와 같이 2x2 행렬 형태를 가지고 있다. 여기서 y가 취할 수 있는 값은 분류 문제이기 때문에 0과 1이다. 예를 들어 '남자'인지 '여자'인지를 맞추는 분류문제가 있다고 해보자. 여기서 남자를 0으로, 여자는 1로 데이터가 정의되어 있다고 가정해 보겠다. 그러면, 종속변수 y가 취할 수 있는 값은 0과 1일 테고, 여자를 기준으로 여자면 1, 여자가 아니면 0이라고 말할 수 있다. 실제 train 데이터에서의 0, 1 데이터와 학습시킨 모델이 test data에 대해 예측한 0, 1 데이터가 어느 정도 차이가 있을 것이다.(정확도가 100%가 아니라면)
| True Negative(TN) | False Positive(FP) |
| False Negative(FN) | True Positive(TP) |
이제 다시 위 표를 살펴보자. TN은 실제 y의 값이 0인데(여자X), 예측된 y값도 0인 경우이다. 마찬가지로 TP는 실제 y값이 1이고(여자 O), 예측된 y값도 1인 경우이다. FP, FN은 각각 실제 y값이 1,0이고, 예측된 y값이 0,1로 못 맞춘 경우이다. 이렇게 경우의 수는 딱 4가지 밖에 없다.
이제 예시를 들어보겠다.
| 8 (TN) | 2 (FP) |
| 5 (FN) | 15 (TP) |
여기서 전체 관측치는 총 30개이다. 실제 맞춘 데이터는 몇개일까? Positive만 count 하면 되기 때문에 17개이다. 마찬가지로, 모델이 정답을 맞히지 못한 데이터는 Nagative만 count 하면 되기 때문에 13개이다. 이 행렬을 분류모델의 성능평가지표인 Accuracy, recall, precision, F1으로 계산해보겠다.
1-2. Accuracy(정확도)
Accuracy(정확도)는 전체 관측치 중에서 정확하게 정답을 맞힌 비중을 나타내는 지표이다. 즉, 식으로 표현하면 아래와 같다.
$$ \frac{TP + TN}{FP + FN + TP + TN} $$
위에서 사용한 예시를 다시 가져와보겠다. 이 표를 계산하면 얼마일까?
| 8 (TN) | 2 (FP) |
| 5 (FN) | 15 (TP) |
전체 관측치가 30개이고, 이 중에 True만 count 하면 23개이다. 그러면 23/30이니까 약 0.76이 나온다.
1-3. Recall(재현율)
Recall(재현율)은 실제 Positive 관측치 중에서 실제로 positive로 예측된 관측치의 비중을 나타내는 지표이다. Recall for positive class로, Sensitivity(민감도)라고 한다. 식으로 나타내면 아래와 같다.
$$ \frac{TP}{TP+FN} $$
다시 표를 살펴보자. 이 표에서 여자가 1(Positive)이고, 남자가 0(Negative)이면, 실제로 여자는 몇 명이고, 남자는 몇 명일까?
| 8 (TN) | 2 (FP) |
| 5 (FN) | 15 (TP) |
정답은 여자는 20명, 남자는 10명이다. FN, FP는 모델이 잘못 맞힌 경우이기 때문에 N -> P, P -> N 으로 바꾸면 실제 값이 나온다. 즉, 실제로 여자를 나타내는 데이터는 TP + FN이다. 그중에 모델이 정답을 맞힌 데이터는 TP이기 때문에 \(\frac{TP}{TP+FN} \) 식이 나왔고, 계산하면 15/20으로, 0.75의 값이 나온다.
반대로 실제 negative 관측치 중에서 실제로 negativ로 예측된 비중도 구할 수 있다. Recall for negative class로, Specificity(특이도)라고 한다. 식으로 나타내면 다음과 같다.
$$ \frac{TN}{TN+FP} $$
계산하면 8/10으로 0.8의 값이 나온다.
1-4. Precision(정밀도)
Positive(또는 negative)로 예측된 관측치 중에서 실제로 Positive(또는 negative)인 관측치의 비중을 나타낸다.(recall과 반대 개념) 식을 살펴보자.
1. Precision for positive class
$$ \frac{TP}{TP+FP} $$
이를 해석하면 도출된 결과가 얼마나 정확한가?를 나타낸다. 다시 표를 보자. 여자로 예측된 관측치(TP + FP) 중에서 실제로 여자인 관측치(TP)를 계산하면 된다. 15/17로, 약 0.88 값이 나온다.
| 8 (TN) | 2 (FP) |
| 5 (FN) | 15 (TP) |
2. Precision for negative class
$$ \frac{TN}{TN+FN} $$
남자로 예측된 관측치(TN + FN) 중에서 실제로 남자인 관측치(TN)를 계산하면, 8/13으로 약 0.61 값이 나온다.
1-5. F1 score
F1 Score는 Precision과 recall의 조화평균을 나타내는 지표이다. 여러 가지 지표 중에 정밀도와 재현율을 모두 다 고려할 수 있는 제일 좋은 평균 계산 방식이 조화평균이기 때문에 일반적으로 조화평균을 사용한다. 식으로 나타내면 다음과 같다.
$$ 2\frac{PRE*REC}{PRE+REC} $$
이 경우에도 Postive를 기준으로 했을 때와 Negative를 기준으로 했을 때를 각각 구할 수 있다. PRE는 Positive를 기준으로 했을 때, 약 0.88, Negative를 기준으로 했을 때, 0.61이 나왔다. REC는 Positive를 기준으로 했을 때, 0.75가 나왔고, Negative를 기준으로 했을 때, 0.8이 나왔다. 이를 계산하면, Positive와 Negative를 기준으로 했을 때, 각각 약 0.81, 0.69 값이 나온다.
이렇게 분류문제에서의 범주형 데이터에 대한 성능평가 지표에 대해 알아보았다. 위에 빨간색으로 표시된 숫자들을 다시 한번 살펴보자. 값이 다 다르다는 걸 눈치챘을 것이다. 그럼 이중에 어떤 지표로 성능 평가를 해야 할까? 일반적으로 재현율과 정밀도 모두 중요하다. 그러나 도메인에 따라 항상 2가지가 동등하게 중요하진 않다. 예를 들어 실제로 암인 사람들 중에서 암에 걸렸다고 예측된 사람들을 나타내는 지표와 암으로 예측이 된 환자들 중에서 실제로 암에 걸린 환자를 나타내는 지표 중에 어떤 게 더 중요할까? 둘 다 중요하겠지만, 전자가 훨씬 중요할 것이다. 암이 아닌데, 암에 걸렸다고 오진단하여 치료를 하는 것보다 암에 걸렸는데, 안걸렸다고 진단을 내리는 경우가 더 치명적인 경우가 많기 때문이다. 그렇기 때문에 도메인을 통해 어떤 게 더 중요한지 생각해 보는 게 필요하다.
2. 데이터 불균형 문제
종속변수가 취할 수 있는 값을 클래스라고 한다. 취할 수 있는 값이 positive와 negative가 있다고 했는데, 이때 학습데이터에 대해서 가지고 있는 관측치의 수가 많이 나는 경우에 이러한 경우를 클래스 불균형 문제라고 한다. 예를 들어 1000개의 학습데이터 관측치가 있다고 했을 때, positive 값을 갖는 관측치가 10개이고, negative 관측치가 990개가 있다면, 클래스 불균형이 있는 것이다.
불균형 문제는 학습이 잘 안 된다라는 문제가 있고, 또 특정한 모형성능 평가 지표가 신뢰도가 떨어질 수 있다.
예를 들어 정확도를 계산해 보자. positive는 90% 정확하게, negative는 100% 정확하게 예측했다고 하면, 아래와 같은 표가 완성되는데, 직관적으로 계산해 보면 정확도가 95%가 될 것 같지만, 사실은 91%의 정확도를 가지게 된다. 즉, 정확도가 positive 데이터에 의존적인 형태가 되어버린다. (반대로, positive를 100%, negative를 90%로 정확하게 예측했다고 가정하면, 정확도는 무려 99.9%가 된다..!)
| TN = 900 | FP = 90 |
| FN = 0 | TP = 10 |
$$ accuarcy = \frac{TN + TP}{TN + FP + FN + TP} = \frac{900 + 10}{900+90+10+0} = 0.91 $$
그래서 불균형 문제가 심각하게 있는 경우엔 정확도의 지표가 신뢰도가 떨어진다. 그래서 이럴 때 재현율, 정밀도, F1을 모두 사용해야 한다. 또한,이 문제를 전처리 단계에서 해결하는 2가지 방법이 있다. oversampling과 undersampling이 그것이다.
2-1. Over sampling
Positive에 속한 클래스의 수를 증가시키는 방법, 즉 10개인 관측치를 990개로 늘리는 방법이다.(너무 극단적인 케이스이긴 하지만..) 가장 간단한 방법은 복사 붙여 넣기가 있다. 하지만 이러한 데이터의 문제는 과적합 문제가 발생할 수 있다. 관측치는 늘지만, 새로운 정보가 추가되지 않기 때문이다. 이러한 단점을 해결하기 위해 일반적으로 많이 사용하는 oversampling 방법은 SMOTE(Synthetic Minority Over-sampling Technique)라는 방법이다. smote의 가장 주요한 특징은 그대로 복붙 해서 증가시키는 것이 아니라, over sampling이 필요한 대상의 정보를 이용해서 새로운 관측치를 생성해서 새로운 관측치의 수를 증가시키는 방법이다. 소수 클래스에 속한 서로 다른 관측치에 대해서 선을 긋고, 선 사이에서 랜덤 하게 하나의 관측치를 뽑아서 새롭게 추가하는 방법이다. 아래 그림에 의하면 초록색 데이터 정보를 합성해서 새로운 빨간색 관측치를 만들어낸다.
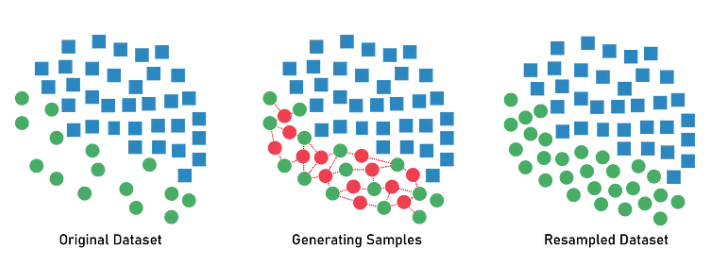
2-2. Under samlping
Under sampling은 많은 관측치를 줄이는 방법이다. Negative가 990개였는데, 10~20개까지 줄여서 숫자를 맞춰주는 것이다. 버리는 방법은 그냥 버리지 않고, 랜덤으로 버린다.
3. 케글 titanic 실습
타이타닉 데이터를 통해 로지스틱 회귀모형을 사용해서 학습을 시키고, 성능평가까지 실습을 해보겠다. 먼저 이 실습을 진행하면서 사용할 라이브러리를 모두 불러오겠다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
sklearn에서 제공하는 여가지 모듈을 불러왔다. 위에서부터 로지스틱 회귀 모형을 불러오는 클래스, train 데이터와 test 데이터를 분리시켜 주는 클래스, 피처스케일링 단계에서 사용하는 표준화 클래스와 min-max 정규화 클래스, 성능평가 단계에서 정확도(accuracy)를 표시하는 클래스, confusion matrix를 보여주는 클래스, 마지막으로 accuracy, recall, precision, F1 score까지 모두 한꺼번에 보여주는 클래스이다.
라이브러리를 불러왔다면, 이제 데이터를 불러올 차례이다. 데이터 케글 사이트에서 다운로드할 수 있다. 경로를 설정하고, train 데이터와 test 데이터를 각각 로드해 준다. (Kaggle Titanic Dataset: https://www.kaggle.com/competitions/titanic/data)
base_path = "/content/drive/MyDrive/Colab Notebooks/data/titanic"
train = pd.read_csv(base_path + "/train.csv")
test = pd.read_csv(base_path + "/test.csv")
참고로, 여기서는 train 데이터에서 성능평가를 위해 따로 분리해 낸 평가데이터의 성능평가를 하는 것까지는 걸 목표로 하기 때문에 사실 test 데이터는 사용하지 않을 것이다. 그럼 이제 train 데이터의 information을 살펴보자.
train.info()
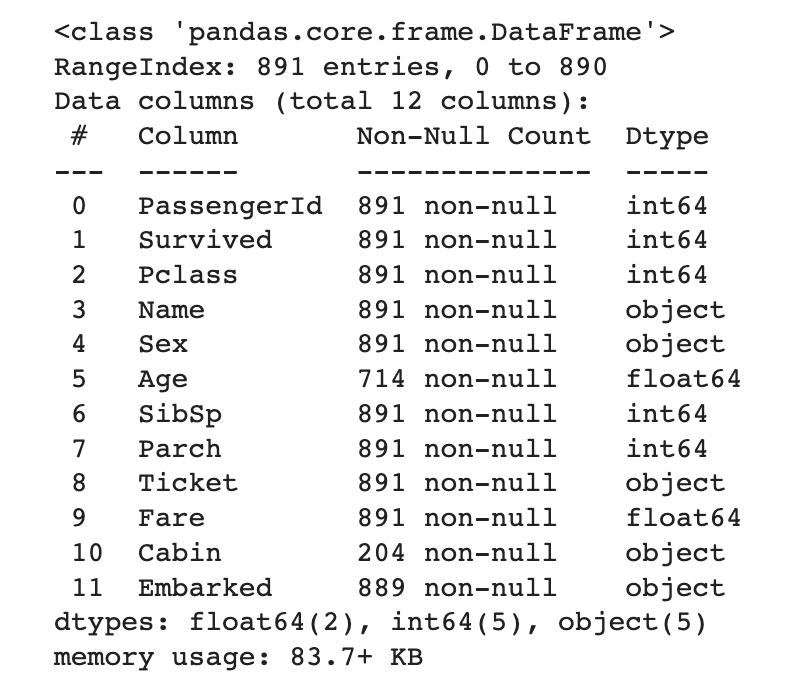
모델 학습을 위해서 빠르게 결측치와 이상치를 제거하고, 피처 스케일링과, 원핫인코딩을 통해 학습을 위한 데이터로 만들어보겠다. 먼저 결측치부터 처리해 보자. 결측치가 있는 Columns는 Age와 Cabin과 Embarked이다. Age는 평균으로 채우고, Embarked는 제일 많은 값으로 채우고, Cabin은 결측치가 너무 많기 때문에 삭제해 주겠다.
train.Embarked.value_counts()
# S 644
# C 168
# Q 77
# Name: Embarked, dtype: int64train['Embarked'] = train.Embarked.fillna('S')
train = train.fillna(train.mean())
train = train.drop('Cabin',axis=1)
Embarked는 'S'가 가장 많아서 'S'로 채우고, 나이는 평균으로 채우고, Cabin은 삭제했다. 다시 information을 보면 모든 Columns가 891개의 데이터를 갖게 된다.
train.info()
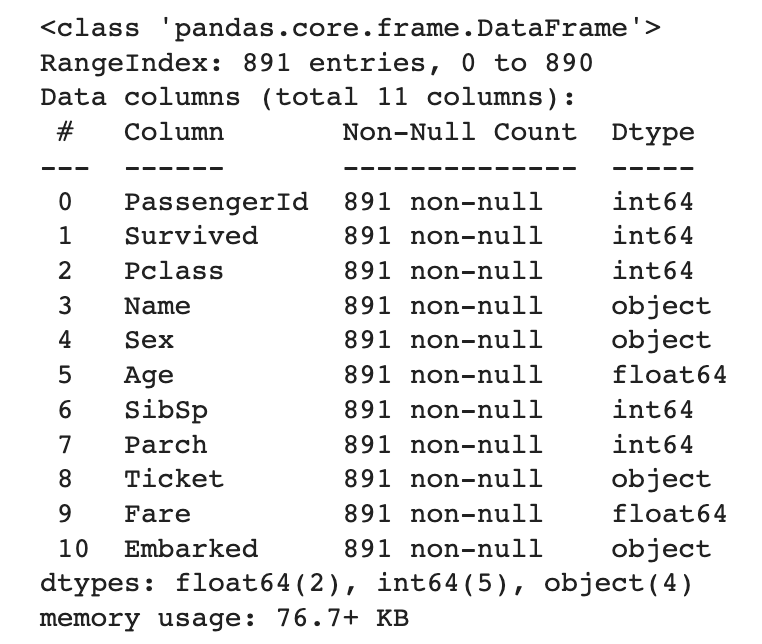
이제 각 column의 유니크 값들이 얼마나 있고, 각각의 유니크 값들이 몇 개가 있는지, 그리고 원핫인코딩이 필요한 column이 어떤 것이 있는지 한꺼번에 확인해 보겠다. (출력 결과는 더 보기 참고)
for col in train.columns:
print(train[col].value_counts())
1 1
599 1
588 1
589 1
590 1
..
301 1
302 1
303 1
304 1
891 1
Name: PassengerId, Length: 891, dtype: int64
0 549
1 342
Name: Survived, dtype: int64
3 491
1 216
2 184
Name: Pclass, dtype: int64
Braund, Mr. Owen Harris 1
Boulos, Mr. Hanna 1
Frolicher-Stehli, Mr. Maxmillian 1
Gilinski, Mr. Eliezer 1
Murdlin, Mr. Joseph 1
..
Kelly, Miss. Anna Katherine "Annie Kate" 1
McCoy, Mr. Bernard 1
Johnson, Mr. William Cahoone Jr 1
Keane, Miss. Nora A 1
Dooley, Mr. Patrick 1
Name: Name, Length: 891, dtype: int64
male 577
female 314
Name: Sex, dtype: int64
29.699118 177
24.000000 30
22.000000 27
18.000000 26
28.000000 25
...
36.500000 1
55.500000 1
0.920000 1
23.500000 1
74.000000 1
Name: Age, Length: 89, dtype: int64
0 608
1 209
2 28
4 18
3 16
8 7
5 5
Name: SibSp, dtype: int64
0 678
1 118
2 80
5 5
3 5
4 4
6 1
Name: Parch, dtype: int64
347082 7
CA. 2343 7
1601 7
3101295 6
CA 2144 6
..
9234 1
19988 1
2693 1
PC 17612 1
370376 1
Name: Ticket, Length: 681, dtype: int64
8.0500 43
13.0000 42
7.8958 38
7.7500 34
26.0000 31
..
35.0000 1
28.5000 1
6.2375 1
14.0000 1
10.5167 1
Name: Fare, Length: 248, dtype: int64
S 646
C 168
Q 77
Name: Embarked, dtype: int64
출력결과를 통해 아래와 같은 결론을 얻었다.(왜 이런 결론을 얻었는지는 더 보기를 참고해 주세요. 단, 제가 정의한 게 정답이라고 볼 수는 없으니 왜 이렇게 사고했는지만 참고해 주시면 감사하겠습니다.)
- PassengerId 제거
- Pclass 원핫인코딩
- Name 제거
- Sex 원핫인코딩
- SibSp -> 2이상부터 하나로 합치기
- Parch -> 2이상부터 하나로 합치기
- Ticket 제거
- Fare 이상치 확인
- Embarked 원핫인코딩
- PassengerId는 모든 값이 유니크한 범주형 문자 데이터이기 때문에 제거.
- Name도 모든 값이 유니크한 범주형 문자 데이터이기 때문에 제거.
- Ticket도 거의 모든 값이 유니크한 범주형 문자 데이터이기 때문에 제거.
- Pclass는 ordinal변수라고 하기엔 조금 애매해서 원핫인코딩.
- Sex는 범주형 문자 데이터이기 때문에 원핫인코딩.
- Embarked도 범주형 문자 데이터이기 때문에 원핫인코딩.
- SibSp는 2 이상부터는 데이터 개수가 너무 작아서 합치기
- Parch도 2이상부터 데이터 갯수가 너무 작아서 합치기
- Fare는 너무 큰 값을 가지는 이상치는 학습에 영향을 줄 수 있기 때문에 제거
PassengerId, Name, Ticket 열을 삭제해 주겠다.
train = train.drop(['PassengerId','Name','Ticket'],axis=1)
Sex, Pclass, Embarked 열을 원핫인코딩해주겠다.
train = pd.get_dummies(train, columns = ['Sex', 'Pclass','Embarked'], drop_first=True)
Sibsp, Parch 열의 2 이상의 값을 2로 통일시켜 주겠다.
train.loc[train['SibSp'] >= 2, 'SibSp'] = 2
train.loc[train['Parch'] >= 2, 'Parch'] = 2
Fare의 이상치를 제거해주겠다. 먼저 boxplot을 통해 너무 많이 벗어난 outliers를 확인하고, 여기서는 임의로 200 이상의 값들을 제거해 주었다.
plt.figure(figsize=(16,6))
sns.boxplot(x=train.Fare)
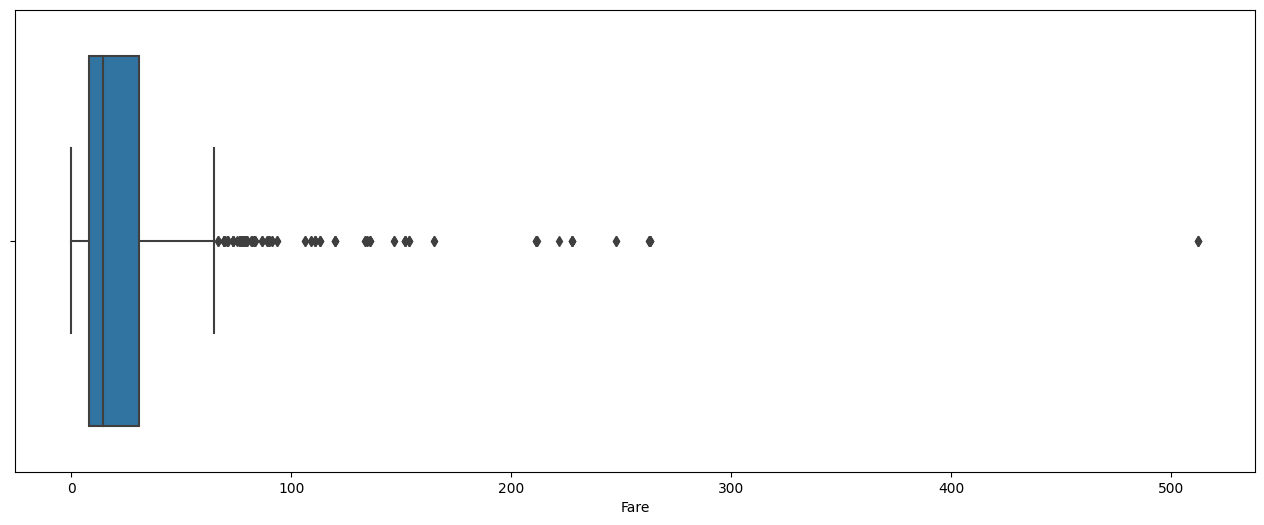
train = train[train.Fare < 200] # 13개 이상치 제거
이제 모델학습을 위한 작업은 끝났다. 여기서부터는 데이터를 분리시키는 작업을 해보겠다. 먼저 독립변수와 종속변수로 분리를 시켜보자.
X = train.drop('Survived', axis=1)
y = train.Survived
그리고 학습을 위한 데이터와 평가를 위한 데이터로 분리시키겠다.(왜 분리시키는 건지 모르겠다면, 이 글의 4-2 파트를 참고하도록 하자.)
from sklearn.model_selection import train_test_split
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)
train데이터의 독립변수를 표준화, min-max 정규화 방법을 통해 피처스케일링을 각각 시켜보겠다.(피처 스케일링 관련해서는 이 글을 참고하면 된다.)
scaler = StandardScaler()
mm_scaler = MinMaxScaler()
X_train_std = scaler.fit_transform(X_train)
X_val_std = scaler.transform(X_val)
X_train_minmax = mm_scaler.fit_transform(X_train)
X_val_minmax = mm_scaler.transform(X_val)
이제 모든 준비가 끝났다. 바로, 모델을 학습시키고 성능평가를 해보자. (로지스틱 회귀 관련 글(실습포함))
lr = LogisticRegression(C=0.1, penalty='l1', solver='saga', max_iter=1000)
lr.fit(X_train_minmax, y_train)
여기서는 표준화보다 min-max 정규화가 더 성능이 높게 나와서, minmax 정규화 방법을 선택했다. 케글 사이트에 보면, 점수는 accuracy로 측정한다고 나와있다. 그럼 바로 accuracy 먼저 체크해 보자.

lr.score(X_val_minmax,y_val)
accuracy 구하는 방법은 아주 간단하다. score함수를 사용하면 된다. 아래와 같은 방법으로도 똑같이 accuracy를 구할 수 있다. 여기서는 accuracy가 0.8이 나왔다.
y_predictions = lr.predict(X_val_minmax)
accuracy_score(y_val, y_predictions)

counfusion matrix도 확인해 보겠다.
confusion_matrix(y_val, y_predictions)
# array([[88, 14],
# [21, 52]])
마지막으로 accuracy, recall, precision, F1 score까지 모두 한꺼번에 확인해 보자.
print(classification_report(y_val, y_predictions))
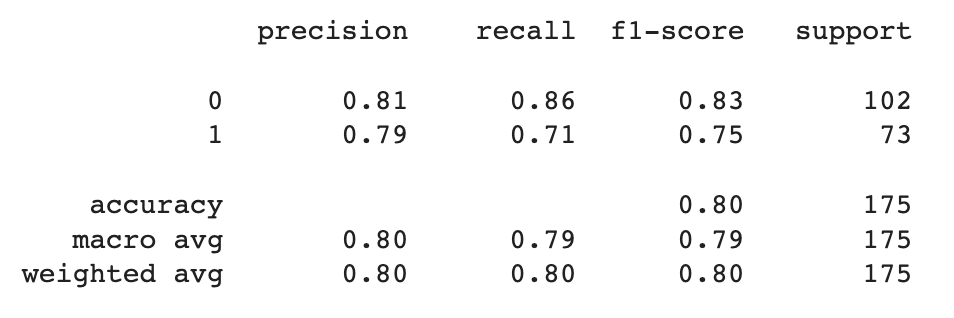
여기서 support를 먼저 해석하면, 평가 데이터가 총 175개이고, 그중에 실제로 0인 값이 102개, 1인 값이 73개라는 뜻이다. macro avg는 각각 지표의 평균을 나타낸다. 예를 들어 precision을 보면, 0은 0.81이고, 1은 7.9의 성능이 나왔다. 이 2개의 성능을 더해서 2로 나눈 0.8 값이 macro avg이다. (\(\frac{1}{2}(0.81 + 0.79)=0.8\))
weighted avg는 실제 값의 개수에 따라 각 클래스의 점수에 가중치를 부여하여 평균을 계산한 가중평균을 나타낸다. 예를 들어 recall이 0일 때, 0.86이 나왔고, support 개수는 102이다. 그리고 1일 때, 0.71이 나왔고, support 개수는 73개이다. 이를 계산하면, 약 0.8이 나온다. (\((102\times0.86 + 73\times0.71)\frac{1}{175}\cong0.8\))
일반적으로 각각의 클래스에 관측치 수의 차이가 많이 나는 경우 macro avg 지표가 더 선호된다. 관측치의 수가 클래스별로 많이 나는 경우에 weighted avg를 사용하게 되면 모형의 성능이 더 좋게 나올 수밖에 없기 때문이다. 그래서 좀 더 객관적인 모형의 성능을 파악하기 위해서는 macro avg를 사용하는 게 보수적인 지표로 더 바람직하다.
'머신러닝,딥러닝 > ML 회귀분석(이상엽 교수님)' 카테고리의 다른 글
| ROC curve, AUC 개념 및 sklearn 코드 (1) | 2023.06.15 |
|---|---|
| [로지스틱 회귀] Solver 종류와 장단점 (2) | 2023.06.07 |
| 원-핫 인코딩: pd.get_dummies() vs OneHotEncoder() (2) | 2023.06.06 |
| 로지스틱 회귀 모형: 함수 개념 및 코딩 실습 (0) | 2023.05.29 |
| 회귀모델: 라쏘(Lasso), 릿지(Ridge), 엘라스틱 넷(ElasticNet) (0) | 2023.05.29 |



댓글