목차
알고리즘(Algorithm)이란?
1. 정렬 알고리즘(Sorting algorithms)
1-1. 버블 정렬(Bubble sorting)
1-2. 퀵 정렬(Quick Sort)
2. 탐색 알고리즘(Searching algorithms)
2-1. 선형 검색(Linear Search)
2-2. 이진 탐색(Binary Search)
알고리즘(Algorithm)이란?
컴퓨터공학에서의 알고리즘이란 어떠한 문제를 해결하기 위해 정해진 일련의 절차나 방법을 공식화한 형태로 표현한 것입니다. 일반적으로 알고 있는 유튜브 알고리즘이랑은 조금 다른 개념입니다. 알고리즘은 입력, 출력, 명확성, 유한성, 효율성의 조건을 만족해야하고, 자연어, 의사코드(pseudo code: 정확하진 않은데 의도만 설명하는 코드), 순서도, 프로그래밍 언어 등으로 표현할 수 있습니다.
좋은 알고리즘을 설계하기 위해서는 공간복잡도와 시간복잡도를 고려해야합니다.
알고리즘의 구현을 위해서 자주 사용하는 접근 방식 2가지가 있습니다. 재귀(Recursion)와 반복(iterative)입니다. 재귀 방식은 함수내에서 파라미터를 바꿔 새로운 자기 자신을 호출하는 방식입니다.

재귀 방식을 이용하는 경우 반복 방식보다 코드가 간결하고 가독성이 좋아서 문제를 쉽게 이해할 수 있다는 장점이 있습니다. 하지만 그 과정에서 일어나는 계속적인 함수 호출은 스택에 함수 호출과 복귀 위치 등의 정보를 계속해서 추가하기 때문에 스택 오버플로우 문제가 발생할 수 있고, 시스템에 부담을 주기도 합니다.(이러한 문제들을 해결을 위해 스택오버플로우 커뮤니티가 생겨난듯하다..)

이미 우리에게 익숙한 방식은 반복을 적용한 알고리즘입니다. for문, while문과 같은 loop 반복문을 통해서 문제를 해결할 수 있죠. 이 경우에는 스택 오버플로우 문제가 없고, 시스템적 부담이 적다는 장점이 있지만 코드가 복잡해진다는 단점이 있습니다.
그럼 알고리즘 중에서도 대표적인 정렬 알고리즘과 서칭 알고리즘에 대해 알아보겠습니다.
1. 정렬 알고리즘(Sorting algorithms)
정렬 알고리즘은 주어진 데이터를 정해진 순서대로 재배열하는 알고리즘입니다. 순서대로 재배열을 하려면, 비교 기준이 있어야합니다. 예를들어, 도서관의 책을 정리할 때, 제목의 첫 글자 자음 ㄱ,ㄴ,ㄷ,ㄹ 순으로 정렬을 할지, 책 발행일 순으로 정렬을 할지 등의 기준이 있어야하겠죠. 또는 서울, 부산의 위치를 비교해본다고 가정해보겠습니다. 이때는 '위치'라는 비교 기준이 있긴 하지만, 그 위치를 비교하려면, 위치를 나타낼 수 있는 명확한 수치가 필요하겠죠. 위도와 경도까지 표시할 수있는 좌표 번호를 데이터로 표기할 수 있게 정의가 되어있야 위치를 비교할 수 있습니다.
정렬 알리즘은 이렇게 비교 기준에 따라 데이터를 정렬시킬 때 사용됩니다. 우리가 쓰는 소프트웨어 중 정렬이 들어가지 않는 곳이 없을 만큼 자주 쓰이는 알고리즘입니다. 데이터베이스 검색, 데이터 분석, 검색 엔진 등에서 주로 사용되며, 우리는 메일 보관함, 쇼핑몰, 뉴스피드 등이 정렬되어있는 모습을 보면서 정렬 알고리즘이 적용되어있음을 확인할 수 있습니다. 정렬 알고리즘은 다양한 종류가 있지만 여기서는 대표적인 정렬 알고리즘 4가지를 살펴보겠습니다.
1-1. 버블 정렬(Bubble sorting)
버블 정렬은 인접한 두 원소를 비교하여 조건에 따라 위치를 변경하는 방법입니다. 오름차순 기준으로, 인접한 두 원소를 비교하면서 큰 값을 뒤로 보내며 정렬이 이루어집니다. 가장 큰 값을 가장 마지막으로 보내는 것이 한 번의 스텝으로 보고, 한 번의 스텝이 끝나면 아래 그림과 같이 뒤에서부터 정렬되는 것을 볼 수 있습니다.
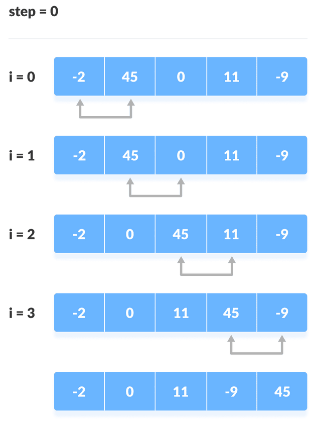
데이터가 총 N개라면, Step = 0일 때, N-1번비교하고... Step = N-1일 때, 1번 비교할 때까지 반복해야하므로, O(N^2)의 시간 복잡도를 가집니다. 데이터가 어느정도 정렬이 되어있는 상황이라면, swap이 많이 일어나지 않아 효과적이지 않은 방식입니다.
# 파이썬으로 구현하는 버블 정렬
def bubble_sort(L):
N = len(L) # 데이터의 갯수 : 5
for i in range(N): # 0,1,2,3,4
for j in range(N-i-1): # 4,3,2,1
if L[j] > L[j+1]: # L[4] L[5] # Indexerror (boundary condition)
L[j], L[j+1] = L[j+1], L[j] # swap
return L
L = [-1, 45, 0 ,11, 9]
print(bubble_sort(L)) # [-1, 0, 9, 11, 45]# O(N * logN)
L.sort() # L 자체가 정렬이 된다.
print(L) print(sorted(L)) # L 자체가 정렬이 되진 않고, 정렬된 결과만 return.
1-2. 퀵 정렬(Quick Sort)
퀵 정렬은 분할 정복(divide and conquer) 방법을 사용하여 주어진 리스트를 정렬하는 알고리즘입니다. 평균적으로 O(nlogn)의 가장 빠른 시간 복잡도를 가지고 있어 널리 사용되지만, 최악의 경우 O(n^2)의 시간복잡도를 가집니다.
분할 적복이란 복잡한 전체의 문제를 부분으로 나누어, 부분적인 문제를 해결하고 다시 합쳐 전체를 해결하는 방식을 의미합니다. 이 과정에서 분할 된 리스트의 크기가 작아질수록 더 빠른 속도를 보이는 효율적인 알고리즘입니다.
퀵 정렬 알고리즘 구현
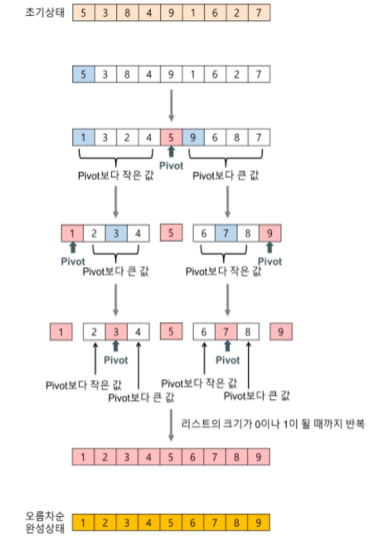
1) 리스트에서 하나의 원소를 선택합니다. 이를 피벗(pivot)이라고 합니다.
2) 피벗을 기준으로 작은 값은 외쪽, 큰 값을 오른쪽으로 리스트를 두 개로 분할합니다.
3) 피벗을 기준으로 왼쪽 리스트는 모두 피벗보다 작거나 같은 값을 갖도록, 오른쪽 리스트는 모두 피벗보다 큰 값을 갖도록 정렬합니다.
4) 분할된 두 개의 작은 리스트에 대해 재귀적으로 퀵 정렬을 수행합니다.
5) 재귀 호출이 더 이상 분할이 불가능할 때까지 반복합니다.
이 외에도 선택 정렬(Selection Sort), 삽입 정렬(Insertion Sorting) 등이 있습니다. 선택 정렬은 주어진 리스트에서 최솟값을 찾아 맨 앞에 위치한 값과 교체하고, 그 다음 최솟값을 찾아 두 번째 위치한 값과 교체하는 과정을 반복하는 방식입니다. O(N^2)의 시간복잡도를 가지며, 입력 배열이 이미 정령되어 있건 말건 관계없이 동일한 연산량을 가지고 있기 때문에 최적화 여지가 적어서 다른 정렬 알고리즘과 비교해봤을 때도 성능이 떨어지는 편입니다. 삽입 정렬은 각 숫자를 적절한 위치에 삽입하여 정렬하는 알고리즘입니다. 마찬가지로 O(N^2)의 시간복잡도를 가집니다.
2. 탐색 알고리즘(Searching algorithms)
탐색 알고리즘은 리스트에서 원하는 항목을 찾는 알고리즘입니다. 여기서는 대표적인 서칭 알고리즘인 선형검색(Linear seach)과 이진 탐색(Binary Search) 두 가지를 살펴보겠습니다.
2-1. 선형 검색(Linear Search)
선형검색은 순차탐색, 전탐색이라고도 불리며, 리스트, 배열 등 선형구조에서 찾고자 하는 항목을 순차적으로 탐색하는 방법의 검색 알고리즘입니다. 리스트가 정렬되어 있지 않아도 사용할 수 있지만, for문을 이용해서 앞에서부터 원하는 값을 찾기 때문에, 시간 복잡도가 O(N)으로 비교적 느리다는 단점이 있습니다.(즉, 데이터를 다 본다는 뜻이기 때문에, 서치에서는 최악이라고 볼 수 있습니다.)
# 파이썬으로 선형 검색 알고리즘 구현
def linear_search(arr, x):
"""
arr : 리스트
x : 찾고자 하는 값
result : return value, 찾은 값의 index
"""
n = len(arr)
for i in range(n):
if arr[i] == x:
return i
return -1 # 찾는 값이 리스트에 없을 경우
# returen result
# 예시
arr = [1, 3, 5, 7, 9]
x = 7
result = linear_search(arr, x)
if result == -1:
print("찾는 값이 리스트에 없습니다.")
else:
print(f"{x}은(는) 리스트의 인덱스 {result}에 위치합니다.")
2-2. 이진 탐색(Binary Search)
이진 탐색은 이미 정렬된 리스트에서 원하는 항목을 찾는 알고리즘입니다. 정렬된 데이터셋(이진 트리, 배열)에서 탐색 범위를 반으로 줄여가면서 원하는 항목을 찾습니다. 시간 복잡도는 O(log N)으로 큰 효율성을 가지지만, 정렬된 리스트에서만 사용할 수 있다는 단점이 있습니다.
이진 탐색 알고리즘 구현
1) 리스트의 중간 값을 선택합니다.
2) 중간 값이 원하는 항목보다 크면 왼쪽 반 리스트를, 작으면 오른쪽 반 리스트를 선택합니다.
3) 선택된 반 리스트에서 다시 중간 값을 선택합니다.
4) 위의 과정을 반복하여 원하는 항목을 찾을 때까지 계속합니다.
마무리
여기까지 대표적인 정렬 알고리즘 4가지와 서칭 알고리즘 2가지를 살펴보았습니다. 정렬 알고리즘과 서칭 알고리즘은 컴퓨터 공학에서 매우 중요한 개념이며, 알고리즘을 공부하는 것은 컴퓨팅 사고력(Computaional Thinking)을 키우는 가장 좋은 공부 방법입니다. 알고리즘을 구현할 때는 주어진 문제의 특성에 따라 적절한 알고리즘을 선택해야 하합니다.
'Computer Science > 컴퓨터공학(김용담 강사님)' 카테고리의 다른 글
| 그래프 자료구조& 알고리즘(BFS, DFS) (0) | 2023.04.08 |
|---|---|
| 트리 자료구조: 이진, 이진탐색, Balanced Tree (0) | 2023.04.08 |
| 자료구조: 배열, 연결리스트, 스택, 큐 (0) | 2023.04.06 |
| 자료구조란? (feat. 시간복잡도, 공간복잡도) (0) | 2023.04.06 |
| 추상 자료형(ADT)이란? 개념과 특징 (0) | 2023.04.05 |




댓글