목차
1. 그래프 자료구조
1-1. 그래프 용어
1-2. 그래프 유형
1-3. 그래프 표현
1-3-1. 인접 행렬(Adjacency matrix) 방식
1-3-2. 인접 리스트(Adjacency list) 방식
2. 그래프 알고리즘 개요
2-1. BFS
2-2. DFS
컴퓨터공학에서의 자료구조를 배울 때 목표는 스택, 큐, 트리, 그래프 총 4개의 자료구조를 충분히 이해하는 것입니다. 지금까지 이글을 마지막으로, 총 4개의 파트에 걸쳐서 자료구조를 설명드렸습니다. 이번 글에서는 자료구조 파트 마지막으로 그래프 자료구조를 소개하겠습니다.
1) 자료구조 개념 및 고려사항(시간복잡도, 공간복잡도)
4) 트리 자료구조: 이진, 이진탐색, Balaned Tree
5) 그래프 자료구조
1. 그래프(Graph) 자료구조
그래프는 노드(node)와 노드 사이를 연결하는 간선(edge)으로 이루어진 자료구조입니다. 그래프 자료구조는 현실 세계의 복잡한 구조를 모델링하기 위해 사용되며, 다양한 분야에서 응용됩니다. 대표적인 예로 인스타그램의 팔로우, 팔로워 기능이죠. 트리 구조도 그래프 중 하나에 속합니다.

1-1. 그래프 용어
그래프에서 사용되는 기본 용어는 다음과 같습니다.
- Vertex(=Node, 정점): Tree에서의 Node와 같은 개념
- Edge(=Link, 간선): 정점과 정점을 있는 선
- Weight: 간선의 크기가 있는 경우 그 가중치값
- Degree: 정점에 연결되어 있는 간선의 수
- out-degree: 방향이 있는 그래프에서 정점에서부터 출발하는 간선의 수
- in-degree: 방향이 있는 그래프에서 정점으로 들어오는 간선의 수
- Path: 정점 V_i에서 V_j까지 간선으로 연결된 정점을 순서대로 나열한 리스트 e.g. A → E = {A, B, D, E}
- Path Length: 경로를 구성하는 간선의 수
- Cycle: 경로 중에서 경로의 시작 정점과 마지막 정점이 같은 경로 e.g. A→ A = {A, B, D, A}
1-2. 그래프 종류
무방향 그래프(undirexted graph): 두 정점을 연결하는 간선에 방향이 없는 그래프입니다. 가장 기본적인 모델이죠.

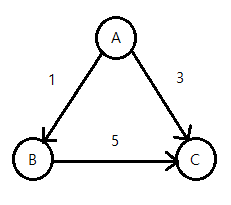
방향 그래프(directed graph): 간선에 방향이 있어 정해진 방향으로만 이동할 수 있는 그래프입니다.

가중 그래프(weighted graph): 간선에 가중치가 부여된 그래프입니다.
1-3. 그래프 표현
그래프 자료구조는 인접 행렬(adjacency list)와 인접 리스트(adjacency matrix) 두 가지 방식으로 표현됩니다.

1-3-1. 인접 행렬(Adjacency matrix) 방식
인접 행렬 방식은 그래프를 이차원 배열로 표현하는 방식입니다. 각 노드 간의 연결 여부를 0과 1로 표현합니다. 이 방식은 노드 수에 비해 간선 수가 많은 경우 효율적입니다. 2차원 행렬이기 때문에 O(V^2)의 메모리가 필요합니다.
1-3-2. 인접 리스트(Adjacency list) 방식
인접 리스트 방식은 그래프를 리스트 형태로 표현하는 방식입니다. 노드 개수만큼 리스트를 만들어 각각의 노드 리스트에 간선을 추가하는 방식입니다. 이 방식은 노드 수에 비해 간선 수가 적은 경우 효율적입니다. O(V+E)의 메모리가 필요합니다.
두가지 방식을 비교하면, 인접행렬 표현은 항상 노드 개수의 제곱만큼의 메모리가 필요한데, 이에 비해 간선이 매우 적으면 비효율적입니다. 또한 탐색을 할 때도 연결되지 않은 간선들도 확인해야 되기 때문데 속도도 느리죠. 하지만 인접 리스는 메모리도 조금만 사용하며, 탐색할 때도 연결된 간선만 보면 되기 때문에 속도도 빠릅니다. 따라서 그래프 자료구조도 상황에 따라 배열과 리스트 중 무엇으로 구현할지 선택해야합니다.
2. 그래프 알고리즘(Graph Algorithm)
앞서 배운 그래프 자료구조는 실생활에도 다양한 분야에서 쓰이는 개념입니다. 도로 정보를 기반으로 최단 경로를 찾거나, 인터넷 네트워크망에서의 전송속도를 계산하는 등 관계 표현이 필요한 경우 그래프를 활용하죠. 그래프 자료구조를 활용한 알고리즘에는 가장 기본적으로 탐색 알고리즘인 BFS와 DFS가 있습니다.
2-1. BFS (Breadth-First Search)
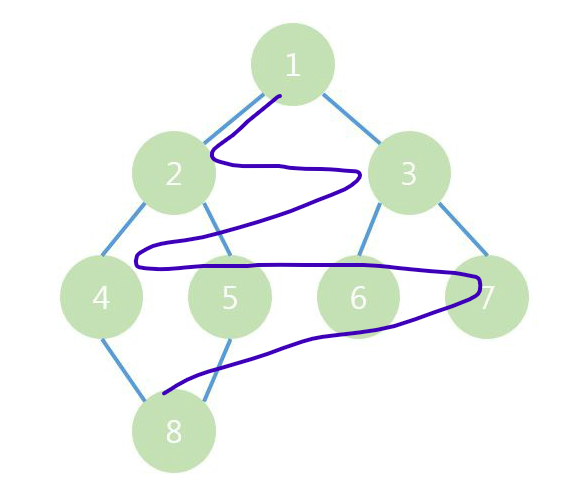
BFS는 너비 우선 탐색 알고리즘입니다. 그래프의 시작 노드부터 인접한 모든 노드를 방문한 후, 다음 단계로 이동하여 깊이가 1씩 증가하는 방식으로 탐색합니다. BFS는 미로찾기같은 최단 경로를 찾는 문제나 가중치가 없는 그래프에서 최소 비용 문제를 해결하는 데 사용됩니다. 구현에 있어서는 방문해야하는 노드를 큐(queue) 자료구조를 통해서 관리합니다. 그림상으로 살펴보면, 아래와 같은 순서로 탐색을 하게 됩니다.
2-2. DFS (Depth-First Search)
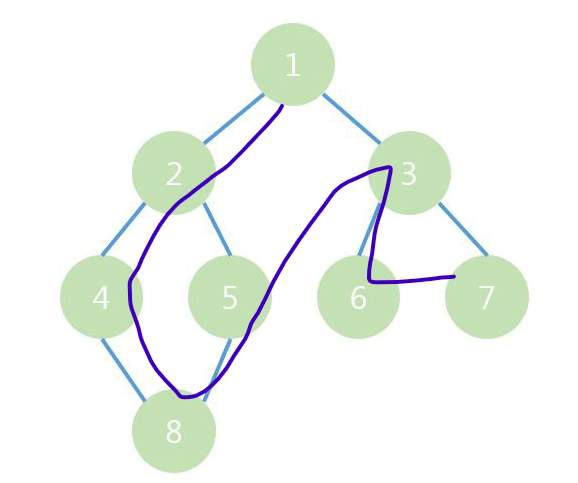
DFS는 깊이 우선 탐색 알고리즘입니다. 그래프의 시작 노드에서 출발하여 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식으로 탐색합니다. 즉, 인접한 노드를 모두 방문한 후, 가장 최근에 방문한 노드로 되돌아와 다음 분기로 탐색합니다. 구현에 있어서는 스택(stack) 자료구조또는 재귀함수를 이용해 구현할 수 있습니다.
여기까지 그래프 자료구조&알고리즘에 대해 알아보았습니다. 감사합니다.
'Computer Science > 컴퓨터공학(김용담 강사님)' 카테고리의 다른 글
| 정수(signed, unsigned)와 부동 소수점 표현 in 컴퓨터 (0) | 2023.04.12 |
|---|---|
| 컴퓨터 아키텍처란: 폰노이만 구조, 명령주기 (0) | 2023.04.09 |
| 트리 자료구조: 이진, 이진탐색, Balanced Tree (0) | 2023.04.08 |
| 정렬 알고리즘(버블, 퀵)과 탐색 알고리즘(선형, 이진) (0) | 2023.04.08 |
| 자료구조: 배열, 연결리스트, 스택, 큐 (0) | 2023.04.06 |




댓글